Magnetic Field due to Current in a Straight Wire

Two very long straight parallel wires, parallel to $y$-axis, carry currents $4I$ and $I$, along $+y$-direction and $-y$-direction, respectively. The wires pass through the $x$-axis at the points $(d, 0, 0)$ and $(-d, 0, 0)$ respectively. The graph of magnetic field $z$-component as one moves along the $x$-axis from $x=-d$ to $x=+d$, is best given by

Equal current i is flowing in three infinitely long wires along positive x, y and z directions. The magnitude field at a point (0, 0, -a) would be:

Find the magnetic field at $P$ due to the arrangement shown.

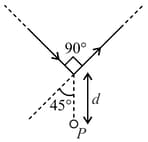
Two mutually perpendicular conductors carrying currents $I_1 \text{and} I_2$ respectively, lie in one plane. Locus of the point at which the magnetic induction is zero, is a:

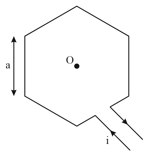
A current $i$ is flowing in a hexagonal coil of side $a$ as shown in the figure. The magnetic induction at the centre of the coil will be:

A long straight wire of circular cross-section (radius $a$) is carrying steady current $\mathrm{I}.$ The current $\mathrm{I}$ is uniformly distributed across this cross-section. The magnetic field is

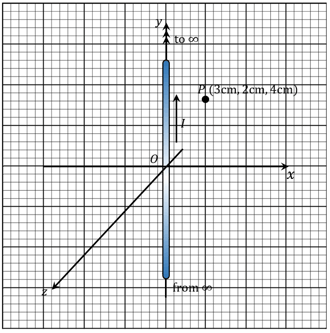
A long straight wire carrying current$i=10 \mathrm{A}$ lies along$y$-axis. Find the magnetic field at $P (3 \mathrm{cm}, 2 \mathrm{cm}, 4 \mathrm{cm}).$

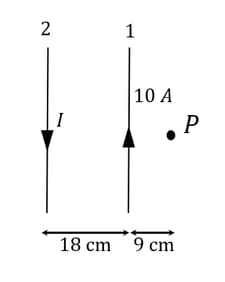
Two parallel infinitely long current carrying wires are shown in the figure. If the resultant magnetic field at point P is zero, then the current $I$ is

The position of point from wire 'B', where the net magnetic field is zero due to following current distribution is

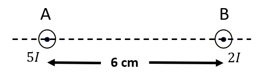
Two infinite parallel wires separated by $1 \mathrm{m}$ carry current $I$ in the same direction. The magnetic field at a point $50 \mathrm{cm}$ from each wire is

Find ${\overrightarrow{B}}_p$ due to the long current carrying parallel wires shown

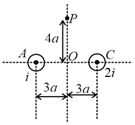
$A,B$ and $C$ wires are given below. Find the ratio of total magnetic field due to $A,B$ and $C$ at points $X$ and $Y$

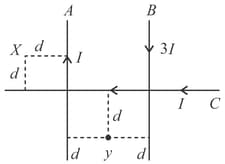
Six very long insulated copper wires are bound together to form a cable. The currents carried by the wires are $I_1=+10 \mathrm{A},I_2=-13 \mathrm{A},I_3=+10 \mathrm{A}$, $I_4=+7 \mathrm{A},I_5=-12 \mathrm{A}$ and $I_6=18 \mathrm{A}$. The magnetic induction at a perpendicular distance of $10 \mathrm{cm}$ from the cable is $\left({\mu }_0=4\pi \times {10}^{-7} \mathrm{Wb} {\mathrm{Am}}^{-1}\right)$

Two long straight wires $A$ and $B$ are placed $50 \mathrm{cm}$ apart and carry current $20 \mathrm{A}$ and $15 \mathrm{A}$ respectively in same direction. A point $P$ is $40 \mathrm{cm}$ from wire $A$ and $30 \mathrm{cm}$ from wire $B$. What is the magnitude of resultant magnetic field at '$P$' in $\left(\mathrm{\mu T}\right)$ unit? $\left(\sqrt{2}=1.414\right)$

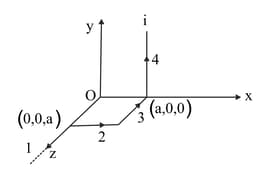
Find $\overrightarrow{B}$ at the origin, due to the long wire, carrying a current $i$.

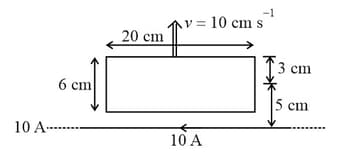
A single coiled rectangular loop of wire with length $20 \mathrm{cm}$ and width $6 \mathrm{cm}$ is placed near to an infinitely long wire carrying current $10 \mathrm{A}$. The loop runs away from the wire with speed $v=10 \mathrm{cm} {\mathrm{s}}^{-1}$ as shown. Find the current in the loop if resistance of wire of loop is $2.5\mathrm{\Omega }$.

Mention the factors the magnetic field due to an infinitely long straight current carrying wire depends upon.

Four infinitely long parallel wires pass through the four corners of a square $PQRS$ of side $a$ that lies in a plane perpendicular to the wires (see figure).

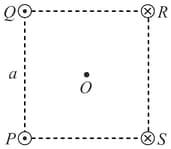
They all carry equal steady currents $I$. Currents in the wires passing through $P$ and $Q$ point out of the page, and the currents in the wires passing through $R$ and $S$ point into the page as shown in the figure. The magnitude of the magnetic field at the centre $O$ of the square is 

Magnetic field at a distance $r$ from an infinitely long straight conductor carrying a steady current varies as

A current of $45 \mathrm{A}$ is passing through an infinitely long wire which lies along the axis of an infinitely long solenoid of radius $1 \mathrm{cm}$. The magnetic field produced by the solenoid in the direction of the current in the wire is $4\mathrm{mT}$. What is the approximate magnitude of the resultant magnetic field at a point $3 \mathrm{mm}$ radially away from the solenoid acis? (Use ${\mu }_0=4\pi \times {10}^{-7} \mathrm{T} \mathrm{m}/\mathrm{A}$ )